1. Introduzione

L’addizione di due numeri binari A e B può essere ottenuta per mezzo della relazione

C0 = 0

Si = Ai xor Bi xor Ci [ Somma ( Sum )]

Ci+1 = Gi or ( Pi and Ci ) [ Riporto (Carry) nel bit i+1 ]

dove

Pi = Ai xor Bi [ segnale di Propagazione ( Propagate ) ]

Gi = Ai and Bi [segnale di Generazione ( Generate ) ]

i = posizione del bit a partire da quello meno significativo dell’adder (LSB)

In un semplice sommatore ripple carry il ritardo nel caso peggiore è proporzionale alla sua dimensione, perché se un riporto è generato nel LSB esso sarà propagato attraverso l’intera struttura.

Possiamo dividere il numero totale di bit in gruppi ed applicare le seguenti regole ad ogni gruppo:

· Se ogni Ai # Bi in un gruppo , allora non abbiamo bisogno di calcolare il nuovo valore di Ci+1 per il blocco; il carry-in del blocco può essere propagato direttamente al prossimo blocco.

· Se Ai = Bi = 1 per qualche i nel gruppo , è generato un riporto che può essere propagato fino all’uscita del gruppo.

· Se Ai = Bi = 0 , non sarà propagato un riporto dalla locazione del bit.

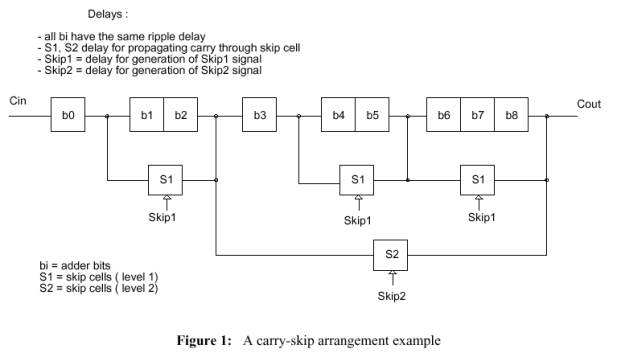
L’idea di base del carry-skip adder è di controllare se in ogni gruppo tutti gli Ai # Bi e permettere al carry-in del blocco di saltare (skip) il blocco quando si verifica questa situazione. In generale un ritardo di un block-skip, può essere differente dal ritardo introdotto dalla propagazione del riporto nella prossima posizione di bit.

Nel caso di un adder ad un solo livello di skip, dobbiamo generare per ogni gruppo un segnale Skip1 , che è semplicemente la logica and di tutti i Pi in quel blocco . Skip1 abiliterà la cella di skip a propagare il carry-in del gruppo direttamente all’ingresso del prossimo gruppo.

Skip1 = Pn and Pn-1 and ….. and P1

n = numero di bit nel gruppo

Il ritardo totale del sommatore, sarà dato dal caso peggiore del ritardo di propagazione del riporto più il ritardo di produzione dell’ultimo bit di somma ( Sum ).

Il problema, dato il ritardo dello skip e del ripple , è di trovare la dimensione del blocco che minimizza il ritardo nel caso peggiore. Il concetto può essere applicato ricorsivamente in un sommatore carry-skip ad n-livelli, allo scopo di ottenere un sommatore carry-skip ad (n-1)-livelli con le celle di skip controllate dai segnali:

Skip2 = Skip1n and Skip1n-1 and . . . and Skip11

. . . and . and . . . and .

Skipm = Skipmn and Skipmn-1 and . . . and Skipm1

dove Skipij è il j-esimo segnale al livello i

Sono stati scritti molti articoli sulla scelta dei gruppi di skip, ma tutti trattano il problema senza considerare alcuni importanti dettagli. Essi restringono la trattazione, a volte implicitamente, ad una particolare implementazione ed ad un caso di esempio , come quello di un carry-skip adder ad uno o due livelli. Nell articolo di Lehman e Burla la configurazione migliore è ricavata per gruppi di dimensione uguale; Majerski studiò anche il problema e Guyot, Hochet e Muller ridussero l’ottimale distribuzione del gruppo alla soluzione di un problema geometrico. Nell’ articolo di Oklobdzija e Barnes è descritto un metodo per determinare la divisione ottima di una catena di riporto. Sono anche descritti esempi per carry-skip ad uno e due livelli, ma i metodi non possono essere applicati se i ritardi delle differenti celle non soddisfano alcune limitazioni. L’algoritmo proposto qui supera le seguenti limitazioni dei metodi precedenti:

· Anche le distribuzioni asimmetriche possono essere generate. Alcuni degli articoli considerano solo distribuzioni simmetriche.

· È presa in considerazione la possibilità di avere un carry-in nel bit di ordine basso dell’adder, consentendo performance efficienti di due dei complementi aritmetici.

· Possono essere assegnati ritardi differenti alle celle di ripple ed alle celle di skip ad ogni livello di carry skip. Non ha importanza quale tecnologia consideriamo,il nodo alla fine di un blocco, dove si fondono due o più percorsi di riporto ,ha una capacità maggiore di quella dei nodi intermedi nella catena di riporto. Questo implica che il ritardo associato alle celle che pilotano questo nodo è maggiore in tecnologie come la CMOS ,dove le porte devono essere ridimensionate per ottimizzare le performance, o in tecnologie come l’ ECL,in cui la potenza deve essere incrementata a causa di differenti situazioni elettriche.

· Non c’è limitazione al numero di livelli di carry-skip. E’ possibile migliorare le prestazioni del sommatore usando tre o più livelli di skip. Per esempio in CMOS estendendo il numero di livelli di carry-skip a tre ed anche a quattro, ha bassi costi in termini di area e può abbassare il ritardo totale del sommatore del ritardo di una o due gates nel caso di un percorso dati a 32 bit. L’applicazione di questa metodologia all’ECL produce un sommatore che è non solo molto efficiente in termini di area di silicio e consumo di corrente, ma il ritardo totale può essere molto basso a comparabile a quello dei più complessi e costosi sommatori quali carry-look ahead ,conditional sum adder e Ling adder.

· Sono identificate le celle che propagano il riporto più veloce del necessario così da eliminare l’eccesso di velocità o tenerne conto durante il processo di ottimizzazione. Questo è molto utile in ECL, dove il ritardo di una porta è una funzione della potenza dissipata dalla porta stessa.

2. Caso peggiore nel ritardo del riporto

Definiamo l’ordine di un carry-skip adder come il numero di livelli del suo circuito di carry-skip ed un blocco come una qualsiasi distribuzione di bits dell’adder raggruppati assieme e bypassati da una cella di skip. Un blocco ha anche un ordine, che dipende dal livello del circuito di carry –skip connesso ad esso. Nell’esempio di Figura 1 il blocco che contiene i bits b3…b8 , ha ordine due, uguale al più alto livello di celle di skip collocate fra input ed oupot del blocco stesso.

In dipendenza degli operandi forniti, ci sono molti percorsi per il riporto con differenti ritardi di propagazione.Siamo interessati al più lungo ,in quanto rappresenta il caso peggiore nel ritardo di propagazione del sommatore. In generale il percorso del caso peggiore è composto da tre subpercorsi basilari:

· Un riporto è generato all’interno qualche blocco e propagato all’output del blocco stesso , in un tempo proporzionale alla dimensione del blocco stesso. Chiamiamo questo ritardo Dg.

· Dall’output del blocco in cui è stato generato, il riporto salta un certo numero di altri blocchi con un ritardo totale indicato con Ds.

· Finalmente esso termina in un blocco dopo una propagazione attraverso un certo numero di bits con un ritardo De, che è proporzionale alla dimensione del blocco. Poiché siamo interessati al ritardo nel caso peggiore , sarà considerato solamente il percorso più lento compiuto dal riporto.

Il ritardo nel caso peggiore totale Dt, sarà la somma di tre Di:

Dt = Dg + Ds + De

Nell’esempio di Figura 1 un possibile caso peggiore potrebbe essere:

b1 ® b2 ® b3 ® s1 ® b6 ® b7 ® b8

dove un riporto è generato in b1 e propagato fino a b8 attraverso celle di ripple ( bi ) e di skip (Si ).

Ma potrebbe anche essere:

b0 ® S1 ® b3 ® S1 ® b6 ® b7 ® b8

se il ritardo di S1 è più alto della somma del ritardo di ripple attraverso b1 e b2.

Al fine di progettare il sommatore ottimo,la giusta distribuzione dei blocchi così come la loro sistemazione interna che minimizza questo tempo, deve essere trovata per tutte le possibili combinazione degli ingressi

Trovare un algoritmo che, dati il numero di bit dell’adder ed il ritardo associato a tutte le differenti celle, ottimizzi la distribuzione, è un problema hard . E un problema perfino più hard se vogliamo trascurare l’assunzione semplificativa che i ritardi in tutti i possibili percorsi del riporto sono uguali.

Il problema è semplificato se invece di fornire il numero di bit dell’adder e trovare la distribuzione ottima con il ritardo associato al riporto nel caso peggiore , forniamo il ritardo nel caso peggiore per il riporto e cerchiamo la distribuzione ottima per quel ritardo con l’associato numero totale di bit . Variando il ritardo fornito nel caso peggiore, l’algoritmo genererà le distribuzioni ottimali che saranno caratterizzate da un differente numero di bits. Sarà scelta quella con il numero totale di bit uguale o maggiore del valore richiesto dal progetto. Iniziamo questo processo con un ritardo minimo, che è quello richiesto per un gruppo singolo affinché operi correttamente all’assegnato livello di carry-skip,e procederemo fino a che sarà generata l’appropriata distribuzione.

In generale potremmo ottenere distribuzioni che non hanno necessariamente il numero usuale di bit che si incontrano negli adder ( 16 , 32, 64 etc. ), ma possono essere maggiori. Questo significa semplicemente che per un dato ritardo del riporto nel caso peggiore , il numero che otteniamo, rappresenta il numero massimo di bit che può fornire la distribuzione ottima generata . Possiamo eliminare alcune configurazioni di bit al fine di ottenere il numero desiderato senza influire sul ritardo nel caso peggiore. L’eliminazione può essere fatta in accordo con alcune semplici regole che saranno enunciate in seguito.

3. Osservazioni di base sull’algoritmo

L’idea di base consiste nell’assegnare ad ognuno dei blocchi dell’adder, una coppia di ritardi corrispondenti ad una generazione e ad una terminazione del riporto nel blocco. Il ritardo sarà funzione della posizione del blocco lungo il percorso del riporto. Ogni blocco, in accordo con le costrizioni imposte dai ritardi assegnati, conterrà un numero massimo di bits. La combinazione dei ritardi introdotti da tutti i blocchi sarà uguale al ritardo massimo di propagazione del riporto permesso dall’adder.

Partendo con un ritardo del riporto nel caso peggiore assegnato per il sommatore,divideremo in intervalli di tempo in relazione alla posizione del blocco lungo il percorso del riporto, e genereremo la combinazione con il massimo numero di bit. Durante il processo di generazione, che chiameremo espansione del blocco, il percorso per i bit che saranno raggruppati assieme, sarà una funzione del livello di carry-skip assegnato al blocco,anche indicato come ordine del blocco. Se stiamo considerando un blocco di ordine zero, possiamo generare il massimo numero possibile di bit direttamente. Se l’ordine è maggiore ,possiamo considerare il blocco come se fosse un sommatore carry-skip di ordine più basso esso stesso e possiamo applicare ricorsivamente la stessa procedura al blocco. Così, per un livello di carry-skip dato , più alto del banale caso di zero,L’algoritmo genererà un albero i cui nodi corrispondono ai blocchi ed i cui livelli corrispondono ai livelli del carry-skip. Le foglie di quest’ albero saranno i bits dell’adder, e le radici sono i blocchi generati dalla divisione del ritardo totale dell’adder in intervalli di tempo durante la fase iniziale.La struttura ad albero rispetterà la regola in base alla quale da un blocco genitore saranno generati solo i discendenti più prolifici. Questi sono coloro che saranno abilitati a generare il numero più grande di bit. Il percorso che connette le radici al maggior numero di foglie formerà la distribuzione ottima finale.

Al fine di descrivere il funzionamento di un blocco introduciamo una coppia di ritardi ad esso associati. Il primo rappresenta il ritardo massimo consentito al riporto che è generato all’ interno del blocco ed è propagato fino all’uscita.

Il secondo rappresenta il ritardo massimo consentito al riporto che è stato generato in qualche blocco precedente e “muore” nel blocco considerato. Dal significato di questi due valori possiamo assegnare differenti costrizioni al blocco in dipendenza della sua posizione lungo il percorso del riporto. Mentre procediamo lungo il percorso del riporto attraverso i blocchi, il primo numero nella coppia dei ritardi i , sarà incrementato, poichè sarà calcolato più tempo nel caso di una generazione di riporto, mentre il secondo numero, j , sarà decrementato dello stesso ammontare, in quanto un riporto che entra nel blocco ha un ritardo che aumenta tanto più lo prendiamo vicino al carry-out del sommatore. Si vuole anche usare proficuamente il tempo speso nella generazione del segnale Skip di livello più alto usando questo tempo nei blocchi generatori ad un livello più basso dove i corrispondenti segnali di Skip sono pronti . Così la parte iniziale della lista dei blocchi includerà alcuni blocchi di livello più basso per tenere conto di questo fatto.

4. Algoritmo generale

L’algoritmo può essere diviso logicamente in due passi:

· Partizionamento ed assegnamento del ritardo. Partendo con il ritardo totale del riporto, l’insieme di costrizione al livello più alto sarà calcolato ed assegnato ai blocchi corrispondenti.

· Costruzione dell’albero. Sarà generato l’intero albero, partendo dalle costrizioni iniziali assegnate e procedendo verso il basso fino al livello più basso. Il percorso che connette i blocchi generati al passo precedente al numero di bit più grande possibile che può essere derivato dai blocchi stessi , definirà la struttura ottima.

4.1. Partizionamento ed assegnamento del ritardo

Assumiamo in questa sezione e nel resto della trattazione che il riporto si propaga da sinistra verso destra: il bit più a sinistra è il LSB nell’adder. Il partizionamento e l’assegnamento dei ritardi per ogni blocco è un processo in due passi:

Primo passo: Ad ogni livello di carry-skip desiderato, la regola base che determina la generazione del blocco

consiste nel fatto che il ritardo associato con una generazione di riporto sarà lo stesso del ritardo

che avrebbe un riporto se salta quel blocco. Per il primo blocco la situazione è lievemente

differente, differente in quanto il segnale di Skip deve essere pronto prima di usare proficuamente il circuito

di skip. Il ritardo associato ai riporti che scompaiono nel blocco è semplicemente la differenza

fra il ritardo totale del riporto ed il ritardo all’uscita del blocco precedente.

Secondo passo: Nel secondo passo calcoleremo altre coppie di ritardi di livello decrescente, partendo dai ritardi

associati al primo blocco e generati nel primo passo,fino al minimo ritardo possibile per un

riporto generato in un singolo bit. Il valore i nella coppia di ritardi è calcolato aggiungendo il

massimo dei ritardi di Gi e Pi al ritardo della cella di skip a quel livello. La differenza rispetto

alle partizioni generate al primo passo consiste nel fatto che le nuove avranno un livello di

carry-skip più basso. Come detto precedentemente , il livello più basso è motivato dal fatto che il

corrispondente segnale di Skip è già pronto e può essere usato l’opportuno circuito di skip.

4.2 Costruzione dell’ albero

Sarà visitata la lista finale e su di essa si opererà in base al valore del livello di skip della partizione:

Se il livello di skip = 0 : Deve essere generato il giusto numero di bit che soddisfa i ritardi associati alla partizione.

Ciò può essere fatto una volta noti i ritardi per la propagazione e la generazione del riporto

a questo livello. Se il riporto scompare in questo blocco, il massimo numero di bit sarà

determinato dividendo il ritardo dato per il tempo di ripple del riporto ed aggiungendo uno.

Questo perché ,arrivato al circuito di skip, un riporto può propagarsi dal prossimo all’ultimo

bit, altrimenti sarebbe stato intrapreso il percorso di skip. Il ritardo associato ad una

generazione o “uccisione” (kill) di un riporto all’interno di un gruppo di bit è espresso da:

D < = min ( di , dj )

dove

D = massimo ritardo totale di gruppo per un riporto generato o “ucciso” (Kill)

di = massimo ritardo quando un riporto è generato nel blocco

dj = massimo ritardo per la propagazione di un riporto nel blocco prima di essere “ucciso” (Kill)

Per esempio assumiamo che il ritardo associato ai segnali Pi e Gi è un unità di ritardo. Allora per la coppia {3 , 4 } possiamo generare due bit, in quanto in questo caso il primo numero nella coppia ,che è tre, è la costrizione più salda sul numero massimo di bit che soddisfa la relazione in alto. Infatti esso richiede:

1 ( per Pi ) + 2 ( per rippling) = 3 unità di ritardo

per la generazione di un riporto e per la sua trasmissione a cresta (rippling) attraverso due bit.Ora consideriamo la coppia di ritardi {4,2} e le stesse assunzioni sui ritardi. Allora entrambi i valori avrebbero limitato a tre il numero totale di bit che possono essere generati da questa partizione. Questo in quanto esso richiede:

1 ( per Pi ) + 3 (rippling) = 4 unità di ritardo

per la generazione di un riporto nel primo bit e per la sua propagazione attraverso i 3 bits, ma solamente 2 unità per entrare nel blocco e propagarsi dal prossimo all ultimo bit.

Se il livello di skip >= 0 : Questo algoritmo può essere applicato ricorsivamente ad una nuova lista di partizioni un

un livello più in basso che è generata dalla coppia di ritardi data. Solamente la partizione che

genererà il più grande numero di bit sarà scelta come la migliore candidata. Con la lista

delle possibili partizioni sono associati ritardi che variano dal ritardo dato al minimo

ammontare possibile, che è il ritardo giusto relativo ad un bit. Durante questa valutazione,

i ritardi fra i blocchi successivi differiranno del ritardo di una cella di skip un livello in

basso. Per esempio, se assumiamo per semplicità che i ritardi di tutte le celle coinvolte a

a tutti i livelli sono uguali a una unità di ritardo, e partiamo con {4, 5} al livello 2 ,le

possibili scelte saranno:

{2 , 5} {3 , 4} {4 , 3} Insieme di 3 elementi

{3 , 5} {4 , 4} Insieme di 2elementi

{4 , 5} La partizione originale

Il valore 2 nel ritardo di generazione del riporto è stato stabilito considerando che il

ritardo associato con la propagazione del riporto giusto di un bit è:

ritardo di Pi + ritardo di rippling = 1 + 1 = 2

Si può notare che i ritardi differiscono dalle precedenti partizioni di una unità, ma mentre i

ritardi corrispondenti alla generazione del riporto si incrementano, quelli che corrispondono

ad una conclusione del riporto nel blocco si decrementano.

L’insieme che contiene la coppia di ritardi che genererà il più grande numero di bit sarà

scelto come migliore candidato. Nel caso di due insiemi che generano lo stesso numero di

bit , ma differiscono nel numero di elementi, sono possibili varie strategie.

Nel programma sviluppato viene scelto l’insieme con il minore numero di elementi.

Ciò in quanto questa partizione genererà un numero di bit o gruppi di

bit più piccolo.Questo significa che il fan-in delle porte coinvolte nella generazione dei

segnali Skip sarà più basso.

Stampa dei gruppi Quando tutte le partizioni originali hanno generato l’intero albero il processo si ferma,e

l’intera struttura, specificando l’organizzazione dei bit di ogni livello, può essere stampata.

Questa è stata una descrizione generale dell’algoritmo, senza differenziazioni fra ritardi che provengono da partizioni in differenti posti e livelli lungo la lista dei possibili candidati. Nella situazione attuale, i ritardi che corrispondono ad un bit o a gruppi alla fine della lista , possono essere più alti per tenere conto della diversa situazione elettrica dove i differenti percorsi si fondono. Lo stesso discorso si applica ai ritardi delle celle di skip. Si può tenere conto di queste differenze senza cambiare il comportamento di base dell’ algoritmo.

Durante il processo di ricerca della distribuzione ottima con il numero totale di bit richiesto, si forniscono i ritardi del riporto nel caso peggiore incrementati con una generazione più ampia e distribuzioni finali più ampie.L’incremento che è sommato al ritardo nel caso peggiore ad ogni passo deve essere tale che il nuovo insieme di coppie di ritardo genererà distribuzioni con almeno un bit in più. Questo incremento , chiamato adder efficiency incremental delay, o AEID, è definito come Il minimo ritardo incrementale che ,se aggiunto ad ritardo di propagazione del riporto nel caso peggiore, genererebbe una nuova distribuzione con almeno un bit in più.

Un osservazione sull’efficienza di questo algoritmo e che si ha una complessità esponenziale nella costruzione dell’ albero in quanto è ottenuto mediante ricorsione. Tuttavia nei casi pratici fino a 5 o 6 livelli e 128 bit le prestazioni sono molto buone.

4.3. Un esempio

Come esempio consideriamo un adder carry-skip a due livelli e 32 bits, dove il ritardo di ripple del riporto, i ritardi dei segnali Gi e Pi, il ritardo della cella di skip ed i ritardi associati a tutti i segnali Skip sono tutti uguali ad un ritardo unitario. Visto che vogliamo realizzare un carry-skip adder a due livelli , dobbiamo generare i segnali Skip1 e Skip2.

Mostriamo ora una tabella che illustra i ritardi associati ad ogni segnale partendo dall’istante zero.

Segnali	Ritardo totale
Gi , Pi	1
Skip1	2
Skip2	3

ed esso impiega una unità di ritardo per saltare un blocco ad entrambi i livelli.

Per rappresentare i ritardi ed i l livello useremo la notazione { i, j, k }, dove i e j rappresenteranno i ritardi associati alla generazione ed alla terminazione del riporto, mentre k rappresenta il livello della partizione. Assumiamo di iniziare con un ritardo totale di sommatore di 8, la prima lista sarà:

{ 4, 5, 2 } {5, 4, 2} {6, 3, 2 } {7, 2, 2} { 8, 1, 2}

Il valore 4 nella prima partizione rappresenta il ritardo che questo gruppo introdurrebbe nel caso fosse generato un riporto. Il valore 4 deriva dalla considerazione che esso impiega tre unità per generare un segnale Skip2, il quale abilita il primo blocco a saltare il riporto,più un’unità che è il ritardo per l’attuale salto del blocco. Il valore 5 nella prima tripla rappresenta il massimo ritardo permesso per riporti che terminano in questo blocco.Esso è calcolato considerando che il riporto provenendo dal blocco precedente, che farà parte della lista generata al secondo passo,deve avere un ritardo che differirà del ritardo introdotto da una cella di skip rispetto al valore 4, nell’esempio una unità. Questo perché noi vogliamo sempre i ritardi nei percorsi del carry-ripple e del carry-skip siano gli stessi per massimizzare il numero di bit per ogni partizione. Così se sottraiamo dal ritardo totale dell’adder 8, il valore generato dal blocco precedente, che è tre, otteniamo cinque unità.

Gli altri valori sono generati considerando che ad ogni passo lungo la lista, i è incrementato del ritardo di un carry skip a livello e j deve essere decrementato della stessa quantità, in quanto così come si procede lungo la lista, è aggiunta una cella di skip in più. Al secondo passo aggiungeremo nuove partizioni ad un livello più basso e la nuova lista sarà:

{ 2, 8, 0 } {3, 6, 1} {4, 5, 2 } {5, 4, 2} { 6, 3, 2} {7, 2, 2} { 8, 1, 2}

Il valore due nel primo blocco è il minimo ritardo di riporto generato assumendo che la dimensione minima del blocco è due. In questo caso il ritardo è uguale a due unità in quanto abbiamo un’unità di ritardo per Gi o Pi ed una unità di ritardo per la propagazione del riporto attraverso un bit. Il ritardo massimo per la scomparsa del riporto (carry kill delay) è uguale al ritardo di propagazione nel caso peggiore che è stato fornito.

Nel secondo blocco, i è uguale a tre unità e j è calcolato sottraendo il massimo ritardo all’uscita del blocco precedente dal ritardo totale di riporto, che è:

8 - 2 = 6 unità e k = 1

Ora dobbiamo visitare ogni gruppo della lista e per tutti e due calcolare il massimo numero di bit, oppure generare una nuova lista di ritardi per un livello di partizione più basso ed applicare l’algoritmo ricorsivamente. Per il primo gruppo non c’è scelte in quanto possiamo solo generare un bit singolo. Per la seconda partizione , possiamo avere due possibilità:

1 2 oppure 2

che rappresentano due gruppi di uno e due bits rispettivamente con una cella skip ad un livello bypassando ogni gruppo , oppure un singolo gruppo di due bit senza circuito di bypass. Chiaramente la prima scelta genera più bits e perciò sarà selezionata come la migliore candidata. Lo stesso criterio può essere applicato al resto della lista e la tabella in Figura 3 mostra l’espansione di due dei gruppi della lista. Ogni riga indica l’insieme che può essere generato partendo dalla partizione data al livello più alto fino al livello zero. Il gruppo che genera il numero maggiore di bits sarà scelto.

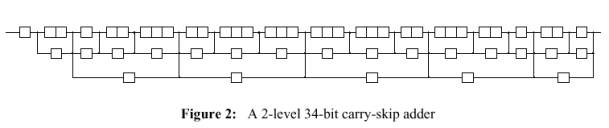
La migliore distribuzione che soddisfa i requisiti con 34 bits è mostrata in Figura 2.

In questo esempio ci sono alcune osservazioni da fare:

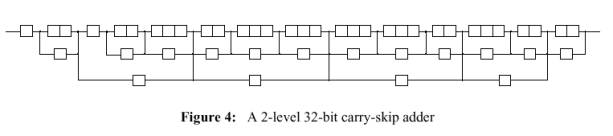
· Il numero totale di bits eccede di due bit rispetto alle dimensioni richieste dell’adder. L’individuazione dei bits da eliminare,può essere basata sulla facilità di implementazione,così come l’abbassamento del massimo fan-in delle porte o l’abbassamento del livello del carry-skip in alcuni blocchi. Nel nostro esempio il massimo fan-in è tre e non cambierà a causa dell’eliminazione di soli due bits ,in quanto ci sono sei gruppi di tre bits. Se l’ultimo bit nell’ultimo gruppo viene eliminato tuttavia,possiamo eliminare un carry bypass a due livelli. La posizione per l’eliminazione del secondo bit è arbitraria. Nell’esempio è stato scelto l’ultimo bit nelle vicinanze dell’ultimo gruppo. Così in Figura 4 è mostrata una possibile distribuzione a 32 bit.

· L’eliminazione di qualche bit non cambia il ritardo di propagazione del riporto nel caso peggiore a meno che l’eliminazione non abbassa entrambi i ritardi associati al blocco di cui i bit sono membri. Come sarà chiarito nella prossima sezione se nell’algoritmo è incluso un test sul numero totale di bit generati ed ad ogni passo il giusto AEID è fornito sempre, per costruzione la precedente distribuzione generata deve avere avuto un numero di bit più piccolo di quello richiesto.Nel nostro esempio ciò può essere facilmente provato dal fatto che l’AEID è costante ad ogni passo ed è uguale al ritardo di una cella di skip al livello più alto, 1 unità nel nostro caso.

Livello	Partizione	Partizione
2	{4, 5, 2}	{5, 4, 2}
1	{ 2, 5, 1 } {3, 4, 1} {4, 3, 1 } { 3, 5, 1 } {4, 4, 1} {4, 5, 1}	{ 2, 4, 1 } {3, 3, 1} {4, 2, 1 } {5, 1, 1 } { 3, 4, 1 } {4, 3, 1} {4, 4, 1 } {4, 4, 1} {5, 3, 1 } {5, 4, 1 }
0	( 1 2 3 ) ® 6 bits ( 2 3 ) ® 5 bits ( 3 ) ® 3 bits	( 2 3 2 1 ) ® 8 bits ( 3 3 2 ) ® 8 bits ( 4 3 ) ® 7 bits ( 4 ) ® 4 bits

I gruppi ( 1 2 3 ) e ( 3 3 2 ) saranno scelti

Figura 3 : espansione di 2 partizioni

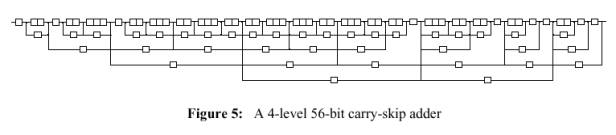
La Figura 5 mostra un altro esempio un carry-skip adder a 4 livelli e 56 bits con le stesse assunzioni circa il ritardo delle celle come nell’esempio a 32bit. Nel diagramma è mostrato che il ritardo del riporto nel caso peggiore è il ritardo di 8 gate come nell’esempio precedente.

Migliorie: AEID e controllo del ritardo di ogni bit

Come è stato definito nella sezione 2, l’AEID è il minimo ritardo di cui deve essere incrementato il ritardo di propagazione del riporto nel caso peggiore , al fine di generare una nuova distribuzione con almeno un bit in più.

Questo garantisce che nel processo di determinare la distribuzione con il giusto numero di bit, ci sarà una perfetta coincidenza fra il numero di bit ed il ritardo di propagazione del riporto nel caso peggiore che questi generano e non sarà sprecato tempo in qualche bit o in gruppi di bit. The AEID è implementato in modo molto semplice. Ogni volta che si genera un blocco, confrontiamo il ritardo che questo blocco sta attualmente generando con i limiti definiti dalla coppia di ritardi. La differenza è comparata con l’AEID precedente e salvata se è minore. Inoltre la differenza fra il ritardo attuale ed il massimo consentito per la configurazione, può essere salvato con il nodo rappresentante la partizione. In questo modo possiamo tenere traccia delle prestazioni in eccesso di alcuni bit e correggere la velocità delle celle coinvolte diminuendo la potenza nel caso di una implementazione in logica ECL , oppure ridimensionando le porte nel percorso nel caso di un progetto a CMOS.